What can undecidability proofs have to do with the Natural Sciences?

Following John Wheeler's approach, the undecidability proofs of Godel, Turing and others which use the self-referential diagonalization argument, force us to choose between demonstrability (physical proof with symbols) and consistency. Quantum mechanics forces us to choose between demonstrability (physical measurement with measurements) and consistency (i.e. unitarity, which evolves consistently each repetition of the experiment). Trivial semantic properties, e.g. a Turing machine that is known to halt in t-steps, correspond to measuring a quantum system in an eigenstate of a chosen observable with probability 1. Oracles are also isomorphic to entangled states. Just as oracles can determine the functional property - like halting versus never halting - for a Turing machine not equivalent to itself, so can a measured quantum system determine the state of an entangled system.

Wheeler's approach simulatenously answers longstanding questions about quantum measurement and quantum cosmology. Wheeler was involved in questions about quantum measurement- his mentor was Niels Bohr and he himself mentored Hugh Everett III. He also pioneered quantum cosmology with the Wheeler-DeWitt equation. In quantum cosmology we want to know how to treat the quantum nature of the universe when the measurement happens within the universe itself (by the very definition of "universe"). Wheeler created his famous self-referential "U-diagram" to describe this - which physicists from Feynman to Maldacena to Witten have warned against dismissing. With regards to quantum measurment, the U-diagram also resolves the question of Bohr versus Everett, by including the measurement (and observer) in the quantum system itself. Formalizing this into the "quantum-diagonalization isomorphism" we see a perfect logical structure i.e. the proofs of Godel, Turing and others, providing a logical structure for quantum measurement without the need to assume anything "metaphysical" beyond what is observed in the laboratory. The "quantum-diagonalization isomorphism" is just data and calculation. We go from "shut up and calculate" to "shut up and diagonalize".

What does this tell us about gravity? Taking the postulates of quantum theory and gravity which do not restrict topologies, we know that at the Planck scale, the topological equivalence (i.e. homeomorphism) problem is undecidable for causal diamonds (intersecting light cones) as causal diamonds are compact 4-manifolds. If placed straddling the horizon of a black hole, one should get an undecidable area, but we know by S=A/4Gh, that the area should be decidable, like Shannon entropy. However it is well-known that the undecidable quantity of Kolmogorov (algorithmic) complexity is asymptotically equivalent to Shannon entropy, the we can treat the semi-classical derivation of Shannon entropy as an approximation.

Several researchers have tried to define living systems in terms of self-reference like Varela (whose work fascinated John Wheeler). Others like Schrodinger tried to define living systems in some hitherto undefined science that is quantum in nature. We use John Wheeler's quantum, self-referential observer as a starting point for defining what living systems in terms of mathematics and physics. Wheeler's Delayed Choice Experiment allows information processors (e.g. observers) to come into existence eons after the Planck Era.

The undecidability proofs of R ~= RE which deals with finite algorithms has its analog with the conjecture P~=NP which deals with feasible algorithms. Can the quantum-diagonalization isomorphism tell us anything new about the three barriers: Relativization (Baker-Gill-Solovay) Algebrization (Aaronson-Wigderson) and Natural Proofs (Razborov-Rudich), since they all have a self-referential character? Can there be any connection to MIP*=RE that connects quantum entanglement with the class RE that is defined by the self-referential proof of Turing?

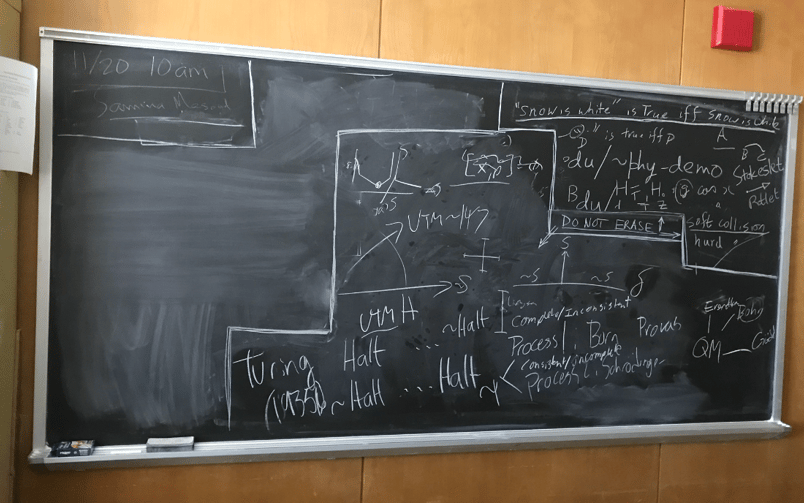
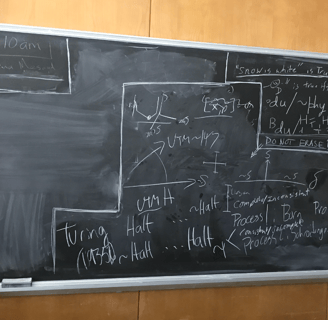
E.C.G. Sudarshan's (UT Austin) Blackboard at the Time of His Passing. Sudarshan, in colorful language, called the development of the connection between Gödel and quantum theory "prophetic" shortly before passing. PMA building, May 2018.

Later Paul Davies (ASU) would call this "Quite obvious" and Rebecca Goldstein (Harvard) would call it "beautiful".

Paul C.W. Davies Hosting the Talk "Wheeler's Vision of a Gödelian Revolution " about the diagonalization-quantum isomorphism and its applications to gravitation and biology.

Feb 7, 2024, Beyond Center for Cosmology at ASU Tempe, Arizona.

Click on title for talk.

Slides here

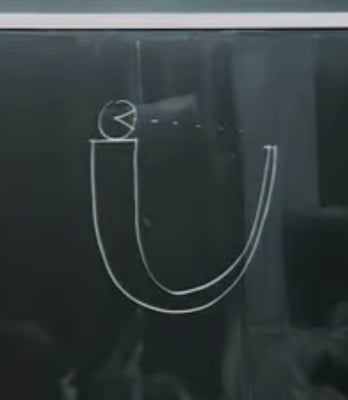
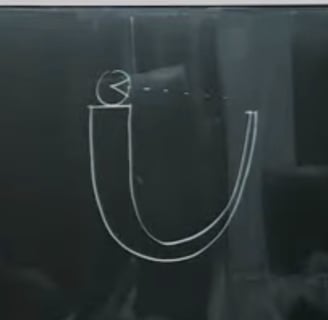
Wheeler's U-Diagram of the Self-Referential Nature of Quantum Theory and Cosmology Source:Quanta Magazine 2017 Interview with Edward Witten (left) and as drawn by Juan Maldacena TASI 2015 (right).

For more on other scientists see:

JAW Centennial (Online)

Working to preserve John A Wheeler's published and unpublished work on an online platform under the auspices of the Wheeler estate. Physical copies of notebooks from the American Philosophical Society, Philadelphia, PA.

JAW Archive (Online)

Exploring the unpublished works of Emil Post (at the American Philosophical Society in Philadelphia, PA) who anticipated the undecidability results of Gödel Turing in 1921, but was academically unaffiliated at times, sometimes teaching high school. Post stated in a postcard to Gödel "As for any claims I might make perhaps the best I can say is that I would have proved Gödel's theorem in 1921- had I been Gödel ". Post also pioneered recursively enumerable sets which inspired Stephen Cook to develop the concept of NP-completeness. Post proved the undecidability of the word problem which connected pure mathematics of topology to logic and questioned the connection between formal logic and the physical world.

Non-Technical Introduction to Undecidability, Quantum Theory and Gravity:

Mad Science Magazine produced for the Mad Science! event at Austin Public Library October 2024

Click here for Magazine

Upcoming Invited Talks:

*Arizona State University (Paul Davies)

*UCLA (Paul Davies)

*University of Surrey (Paul Davies)

*CUNY Graduate School- tentative (Noson Yanofsky)

*Austin Public Library (Public Presentation)

Highlighting implications of undecidability to Planck-scale topology. The topological equivalence (homeomorphism) problem for causal diamonds (compact 4-manifolds) is undecidable, qualitatively equivalent to John Wheeler's "quantum foam".

Uniting two approaches from multiple researchers of defining living systems as either quantum or self-referential into one framework.

Undecidability in Relational Biology as the Framework for Quantum Theory Submitted to Alife Conference in Prague. Reviews here.

Participation with FQXi community

Undecidability as the Framework for Quantum Theory and Spacetime (2020)

This essay is an introduction to the isomorphism between the diagonalization proofs of Godel and Turing and Quantum Theory. Multiple errata, but the ideas are presented here publicly for the first time.

Upcoming Collaborations

On the 1/4 constant of the Bekenstein-Hawking formula with Justin Feng (Central European Institute for Cosmology and Fundamental Physics)

Selected works of John A Wheeler with Dave Kaiser (MIT)

Upcoming Papers

Undecidability of the Homeomorphism Problem for Causal Diamonds and the Planck scale and Black Hole Horizons

The Asymptotic Equivalence of Shannon Entropy and the Expected Value of Kolmogorov Complexity: Can the Area of a Black Hole Horizon be Uncomputable but Approximable?

The Boundary of a Boundary of a Causal Diamond at the Planck Scale: Undecidability, Algebraic Topology and Physics (based on exchange with D. Sullivan CUNY; MTW ch 15)

Prescriptive versus Descriptive Quotation: Logical and Linguistic Approaches to Quotation of Quine and Davidson and Their role in Undecidability Proofs

Godel and Physics written for CUNY graduate school for Noson Yanofsky

Unclassifiability of topology for causal diamonds at Planck scale and no-go theorems in eternal Inflation (based on comments from Paul Davies in Feb 7 2024 ASU talk)

Undecidability, Quantum Theory and the Status of Bohmian Mechanics (written at the request of Sheldon Goldstein, originator of the term "Bohmian mechanics")

Untitled paper on Baker-Gill-Solovay, Aaronson-Wigderson, and Razborov-Rudich barriers in complexity theory

Semiotics of Self-Reference and Paradox

Borges, Mathematics and Physics: An intersection of fiction and foundations of science

From Spinoza to Wheeler: based on exchange with Rebecca Goldstein (Harvard).

Educational Outreach

Discussing science and mathematics of undecidability and quantum theory to a non-technical audience.

Educational Outreach

Mad Science! Paradox in Science and Math! October 31, 2024 Austin Public Library, Austin, TX

Mad Science Magazine!!!

An introduction to undecidability, quantum theory and gravity for children.

"Three Revolutions in the 20th Century" (Changed from original scheduled title of talk) July 3,, PA

Contact Us

Reach out for inquiries about our research and outreach programs.